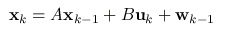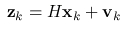Sensor Fusion: The Kalman Filter and its Extensions
This project is about tracking

Overview
Goal of this project is to do a fusion of magnetic and optic sensor data via Extended and Federated Kalman Filters.
The given data consists of positional data
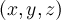
and orientation data given as quaternions
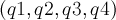
.
For more details on Quaternions and Kalman Filters we refer to the literature below.
Approach
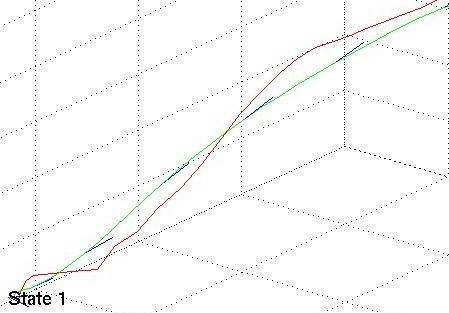
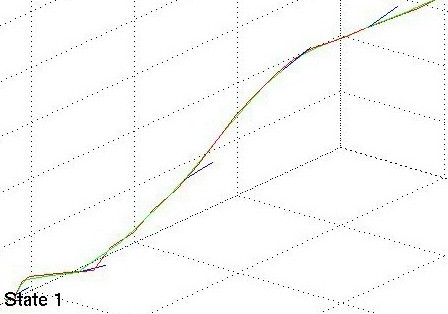
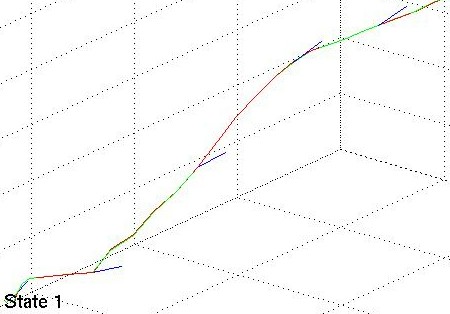
Linear Kalman Filter for position tracking
- Process and Measurement Model
- State Vector: The state vector x is a 9x1 vector containing the positional data (x,y,z), its first and second derivatives (velocity and acceleration) and the orientation data (roll, pitch, jaw) with its first and second derivatives (angular velocity and acceleration).
- Process Model: The process model relates the state at a previous time k-1 with the current state at time k. A is called state transition matrix and w represents the normal distributed process noise with covariance Q. The optinal control input Bu is discarded in the second equation.
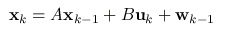

- Measurement Model: The measurement model relates the current state to the measurement z with the matrix H. v is the normal distributed measurement noise with covariance R.
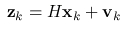

- Kalman Filter Cycle: Prediction and Correction
- Influence of the covariance matrices Q and R
- Q, the process noise covariance, contributes to the overall uncertainty. When Q is large, the Kalman Filter tracks large changes in the data more closely than for smaller Q.
- R, the measurement noise covariance, determines how much information from the measurement is used. If R is high, the Kalman Filter considers the measurements as not very accurate. For smaller R it will follow the measurements more closely.
In the three images below the red lines represent the measurement data, the green lines are the estimated states.
Linear Kalman Filter for position and orientation tracking
Fusion of two 6DOF trackers using the Kalman Filter
- Required: HandEyeCalibration? to align the two tracker coordinate systems
Fusion of two 6DOF trackers using the federated Kalman Filter
Further Steps
- Including noise, EKF
- 5 dof vs 6 dof
- Federated KF
Literature
- R.E. Kalman, A New Approach to linear Filtering and Prediction Problems, 1960
- A. Gelb (editor), Applied Optimal Estimation
- G. Welch and G. Bishop. An Introduction to the Kalman Filter. Technical Report TR 95-041, University of North Carolina, Department of Computer Science, 1995.
- G. Welch: The Kalman Filter Page
- Neal A Carlson, Federated square root filter for decentralized parallel processors, IEEE Transactions on Aerospace and Electronic Systems, Vol. 26 (3) May 1990, pp. 517-525
- G. Welch: SCAAT: Incremental Tracking with Incomplete Information
- David A. Forsyth, Jean Ponce, Tracking with Linear Dynamic Models, Chapter 17 from "Computer Vision: A Modern Approach"
--
KatharinaPentenrieder - 08 Mar 2005

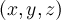 and orientation data given as quaternions
and orientation data given as quaternions 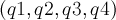 .
For more details on Quaternions and Kalman Filters we refer to the literature below.
.
For more details on Quaternions and Kalman Filters we refer to the literature below.