Pose Inversion
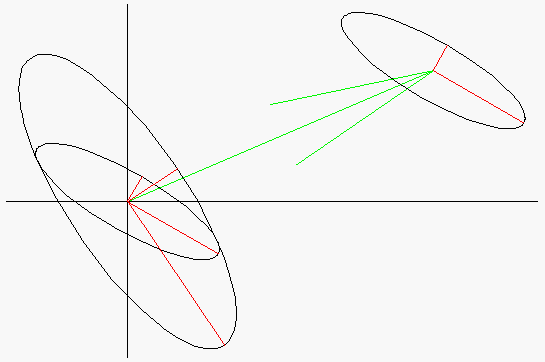
Error propagation for the inversion of a transformation with error
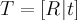 with the corresponding covariance matrix
with the corresponding covariance matrix  , the inverse of the full transformation with error is given by
%$
x^\prime=\left(
\left[\begin{array}{cc}R&t\cr0&1\cr\end{array}\right]
\left[\begin{array}{cc}\Delta_R&\Delta_t\cr0&1\cr\end{array}\right] \right)^{-1}x
=
\left[\begin{array}{cc}\Delta_R&\Delta_t\cr0&1\cr\end{array}\right]^{-1}
\left[\begin{array}{cc}R&t\cr0&1\cr\end{array}\right]^{-1} x
$%
, the inverse of the full transformation with error is given by
%$
x^\prime=\left(
\left[\begin{array}{cc}R&t\cr0&1\cr\end{array}\right]
\left[\begin{array}{cc}\Delta_R&\Delta_t\cr0&1\cr\end{array}\right] \right)^{-1}x
=
\left[\begin{array}{cc}\Delta_R&\Delta_t\cr0&1\cr\end{array}\right]^{-1}
\left[\begin{array}{cc}R&t\cr0&1\cr\end{array}\right]^{-1} x
$%
